阿加塔·乔瓦尼亚·普里马·马克斯,帕拉联邦大学(UFPA)数学与统计学研究生
世界π日
今天,3月14日,是国际π日。
摘要
我们熟知的π值通常是3.14……,它由希腊字母“π”表示。π的本质在于计算圆形和球形图形的面积与体积,这个数字在数学史上极为著名。自2500年前以来,许多伟大的数学家对它的性质和迷人的奥秘表现出浓厚兴趣,长期以来他们尝试计算π的近似值,最终证明π是一个无理数和超越数。这项研究已有超过4000年的记录,涉及多个领域,如几何、分析、代数、概率论、复杂性理论和计算理论等。
本文旨在简要介绍π的历史记录以及一些计算π近似值的方法,探讨古代文明和数学家对π的理解,以及其形式化的过程。
本文采用的方法基于对现有文献的回顾,研究关于π的历史和趣闻的相关资料来源。
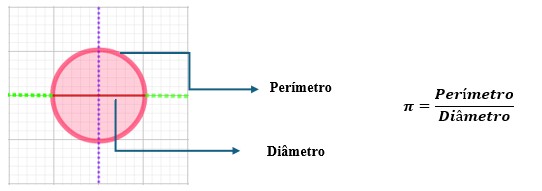
π是一个数学常数,表示圆的周长与其直径的比值。如下图所示:
引言
π早在公元前就已为人所知,并在数学史上占据核心地位。第一次尝试计算π的数值大约发生在公元前。古代数学家多次尝试计算π的近似值,最终证明π是一个无理数,即无法用两个整数的精确比值表示,其小数位无限延伸且不重复。
因此,数学新领域的发展不断扩展,涌现出许多计算π值的新方法,小数位的精度也逐步提高。
这些研究已有超过4000年的记录,涉及几何、分析、代数、概率论、复杂性理论和计算理论等多个领域。

最早研究π的数学家是阿基米德。π的重要性在于它出现在众多科学领域的方程式中(OLIVEIRA; GOMES, 2009)。
π的另一大魅力在于历史上无数次尝试深入理解它的努力。
本文旨在探讨π的历史、重要性及其无理性质,并试图揭示其与数学、计算、历史等领域的奇妙联系,正是这些联系让数学家们数世纪以来为之着迷。
本文采用的方法基于对现有文献的回顾,研究关于π的历史和趣闻的相关资料来源。这意味着研究重点在于分析和综合已出版的书籍、科学文章、历史文献及其他相关材料中的信息。
π日
π日(Pi Day)是国际上纪念数学常数π的日子,每年3月14日庆祝。首次π日庆祝活动由物理学家拉里·肖(Larry Shaw)和旧金山探索博物馆于1988年组织,日期的选择源于美国人记录日期的方式,将3月14日写为3-14,与π的近似值相呼应(这一天也是爱因斯坦的生日)。在2015年3月14日(3-14-15),美国人庆祝了“世纪π日”。
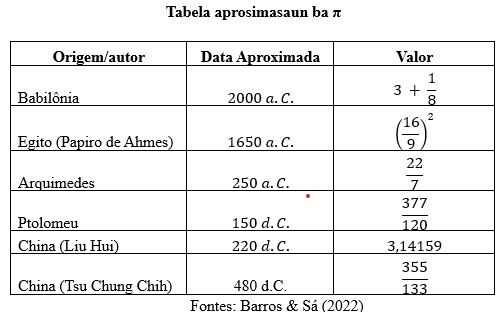
历史上曾多次尝试计算π的近似值。以下表格展示了数学史中不同文明和数学家对π的近似值的记录。
π的历史
π拥有极其迷人的历史,距今已有4000多年。不同时代的众多数学家试图寻找其理性数值,最终发现了令人震惊的事实:无理数的存在。
巴比伦人

大约在公元前17世纪,巴比伦人已掌握先进的数学知识,并将其记录在复杂的泥板上。因此,这些数学天才试图估算π的值并不令人惊讶。
证据来自1936年在伊朗苏萨城发现的泥板。该泥板显示,一个正六边形的周长与外接圆周长的比值意味着π=3.125。
正六边形是一种平面几何图形,具有六个相等的边和六个相等的内角。结论是,根据泥板上的信息,π的近似值被隐含其中(MACHADO, 2013, 引自 BARROS, 2022, p.4)。
埃及

与巴比伦人同时代的埃及人在数学领域也取得了巨大进步。日常生活中,他们使用符号语言表示数学运算,甚至用于计算π。据历史记载,埃及人习惯将粮食储存在圆柱形仓库中。由于圆柱的底面是圆形,掌握一种计算圆面积的方法成为实际需求。这种实际需求提供了一个机会,尽管是隐含地使用π。关于埃及π的证据来自公元前左右的《莱因德纸草书》,其π值约为3.160493(GASPAR; MAURO, 2004)。
中国

在古代中国,π的概念也在探索之中。刘徽,魏国的一名官员,负责审查和解读经典科学文献,包括《九章算术》。基于欧几里得的作品,刘徽开发了一种π的近似方法,其理论是:如果在一个圆内绘制一个多边形,其边数趋于无穷大,则圆的面积与多边形的面积相等。因此,刘徽确定π的近似值为3.14159。
两个世纪后,中国水利工程师祖冲之(430-501年)计算出极为精确的π值,考虑到当时的条件,这一成就令人惊叹。祖冲之的π值在小数表示中非常接近真实值(Blatner, 2001)。
阿基米德
阿基米德利用几何方法构建内接和外接于圆的正多边形,并计算这些多边形的周长。多边形的边数越多,近似值越精确。使用一个96边的正多边形,他得出π的近似值在3.1410和3.1428之间。

他是首位研究π的数学家(公元前287-212年),来自叙拉古,是一位数学家、物理学家、工程师、发明家和天文学家,以经典的π计算方法而闻名。
不同时代的许多数学家不断尝试寻找π的近似值,最终发现了令人震惊的事实:无理数的存在,即无法用两个整数的精确比值表示的数字。
这一证明表明π属于无理数,由约翰·兰伯特于1761年和勒让德于1794年完成。此外,π还是一个超越数,这一性质由费迪南德·林德曼于1882年证明。这意味着不存在以整数或有理数为系数的多项式能以π为根。
由于π是无理数,计算非常困难,其小数表示没有可预测性。![]()
在阿基米德之后,π的计算不断进步,尤其从17世纪开始,随着微积分和无穷级数的发展。如今,π的值可以以惊人的精度计算,达到万亿位小数。由于π是无理数,无法表示为精确分数,其小数表示是无限且非周期的。但有一些分数提供了极佳的π近似值,如下所示:
![]()
π的精确度不断提高,成为一场持续的旅程。随着技术进步,尤其是计算机如ENIAC(电子数值积分计算机)的出现,计算变得更加复杂和广泛,需要更多时间处理π以获得更多小数位。因此,π值的精度随着技术的发展显著提升。1949年,ENIAC耗时70小时计算出2073位精确小数;2002年,日立SR8000超级计算机在602小时内达到1.24万亿位小数,由金田康正完成。
1961年,通过计算得到π的100,265位小数近似值;1967年,达到500,000位小数近似值(Andrade, 1999)。
在欧洲文艺复兴时期,数学领域迎来了新世界,复兴的首要影响是需要找到π的公式。随后发现π的非几何定义在“非几何”角色中发挥作用,即探索其性质和定义,不局限于与圆的关系。从这些值中,最终发现了无穷级数(Santos, 2020)。
从18世纪开始,π开始用希腊字母表示,最早使用π符号的数学家是欧拉(Euler),时间是1736年。欧拉和其他数学家也开始使用这一符号。在其1748年的著作《无穷分析引论》中,符号的使用变得系统化(Lima, 1985)。
据(ONODY 2021)报道,2021年8月14日,瑞士格劳宾登应用科学大学创下新的全球纪录,计算出π的62.8万亿位小数。为了说明这一规模,想象这些数字以大字体打印,仅这些数字就需要大约6280万本书,每本书400页。
π值的重要性
历史上,π是数学中最著名的数字,不同时代的数学天才不断寻求其近似值,既出于好奇,也出于基本需求。π的本质在于计算圆形和球形图形的面积与体积。其相关性扩展到多个科学领域,出现在描述DNA双螺旋、超弦理论、爱因斯坦方程、建筑和几何等众多方程中。此外,π还启发了艺术,如翁贝托·艾柯的小说《傅科摆》和达伦·阿罗诺夫斯基的电影《π:信仰混乱》所示。
关于π的趣闻
- 埃及学家感到欣喜,因为吉萨大金字塔似乎体现了π的近似值。凯奥普斯金字塔的底边长与高度之比,如果将底边长除以两倍高度,得到的值接近π。
- 1995年,后藤博之(Hiroyuki Goto)背诵了π的42,195位小数,创下当时的世界纪录。后来,原口明(Akira Haraguchi)成功背诵了100,000位小数。
- 数学家埃利亚斯·万斯(Elias Vance)在受折磨的情况下,试图基于π的小数位破解代码,以理解资本市场模式。
- 在航行和天文学中,π对于计算天体轨迹和位置至关重要。
此外,π在日常技术中也有应用,如:
- GPS:全球定位系统使用π计算地球几何形状,提供精确位置。
- 电信:π用于与手机信号和其他通信技术相关的计算。
- 计算机图形学:π用于计算机图形算法,创建图像和动画。π的小数位有多少?目前已知π的小数位精确到62.8万亿位!
结论
π拥有极其迷人的历史,距今已有4000多年,其无限且不可预测的性质激发了数学家和科学爱好者的好奇与着迷。其不断增加的小数位成为探索这一数字奥秘和隐藏模式的源泉。π值的精度随着技术进步显著提高,其相关性扩展到多个科学领域,出现在超弦理论、爱因斯坦方程等众多方程中。
通过本文,我们有机会深入了解和掌握数学历史中关于π的知识和理解。
毕竟,这个我们所知的数字在数学史上呈现出极为有趣的维度,对文明本身而言,隐藏着我们从未想象过的惊人方面。
参考文献
Alexandro, V. D. (2017). Em V. D. Alexandro, História e Curiosidade dos Números PI, Número de Ouro e do Número de Euler. Paraná: Fundação Universidade Federal de Randônia-UNIR.
Machado, D. (2013). Propostas Didácticas para o ensino do Número PI. Universidade Federal de Santa Catarina.
Moreno, R. L. (2022). Cálculo de Decimais do número pi. Acesso em 2025, disponível em Minha História do Número Pi: https://www.academia.edu/96226407/Mi_historia_del_n%C3%BAmero_Pi
Onody, R. N. (21 de 10 de 2021). O número Pi com 62,8 trilhões de casas decimais. (IFSC/USP, Ed.) Acesso em 10 de 03 de 2025, disponível em https://www2.ifsc.usp.br/portal-ifsc/o-numero-pi-com-628-trilhoes-de-casas- decimais/
Rafael Lameira Barros, P. F. (2022). INCRÍVEL HISTÓRIA DO NÚMERO PI. Revista Histórica de Matemática para professores, 1-10.
Santos, G. L. (2005). Catolica.udu.br. Em Número π: histórico, sua irracionalidade e transcendência. Universidade Católica de Brasília – UCB. Fonte: https://repositorio.ucb.br:9443/jspui/handle/10869/1877. Acesso em: 05 de março. de 2025
OLIVEIRA, J. C.; GOMES, C. C. Números Irracionais e Transcendentes. 2009. 61 f. TCC (Professor Especialista em Matemática) – Universidade Federal de Santa Catarina e Universidade Virtual do Maranhão, Imperatriz, 2009.
GRILLI, Alexandre; et al. ROTEIRO: Determinando o Número ��. 2011. Disponível em: http://www.gradadm.ifsc.usp.br/dados/20112/SLC0596- 1/Pi%20Roteiro%20Pi.pdf. Acesso em: 08 de março. de 2025.
